Список Художников ►
Эшер

Мауриц Корнелис Эшер
(Maurits Cornelis Escher)
Автопортрет, 1929 г.
Эшер Мауриц Корнелис
(17 июня 1898 — 27 марта 1972, Нидерланды)Нидерландский художник-график
"Иногда, когда я рисую, мне кажется, будто я медиум, находящийся во власти существ, порожденных моим же воображением. Рыбы становятся птицами. День ночью. Из хаоса рождается жизнь, она замирает в мертвых городах, трансформируется в шахматную партию и рассыпается в пыль. Мозаика оживает и превращается в ящериц, они движутся, живут и вновь уходят в орнамент." - Эшер.
Эшер известен прежде всего своими концептуальными литографиями, гравюрами на дереве и металле, в которых он мастерски исследовал пластические аспекты понятий бесконечности и симметрии, а также особенности психологического воспиятия сложных трёхмерных объектов.
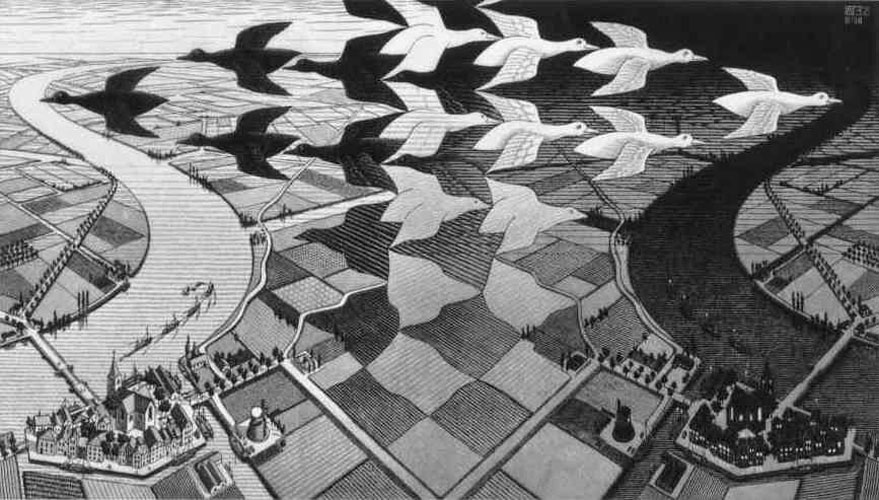
День и ночь, 1938 г.
Гравюра на дереве
День и ночь
Правая и левая часть композиции не только зеркально симметричны, но и как бы служат своеобразными негативами одна другой. По мере того как наш взгляд перемещается снизу вверх квадраты полей превращаются в белых птиц летящих в ночь, и в черных птиц, летающих на фоне светлого дневного неба. Одна субстанция проникает в другую.
Свет и тьма,порядок и хаос оказываются неразрывно связаны. Хаос на одних масштабах может порождать упорядоченность на других и, напротив, хаос в некоторых своих проявлениях выступает как сверхсложная организация.
Попробуем определить границу, на которой кончается день и начинается ночь, где черные лебеди превращаются в белых. Эта граница оказывается в разных местах в зависимости от того, рассматриваем мы картину слева направо или справа налево.
Психологи называют этот эффект бистабильностью восприятия.

Предел - круг III, 1959 г.
Продольная гравюра (две доски). Диаметр 41,5 см.
Предел - круг III
Изогнутые белые линии, пересекаясь, делят друг друга на секции; каждая равна длине рыб - от бесконечны малых до самых крупных, и снова - от самых крупных до бесконечно малых. Каждый ряд монохромен. Необходимо использовать по крайней мере четыре цвета, чтобы добиться тональных контрастов этих рядов. С технологической точки зрения, потребуется пять досок: одна - для черных элементов и четыре - для цветных. Для заполнения круга каждую доску в форме прямоугольного круга следует оттянуть четырежды. таким образом, законченный отпечаток потребует 4х5=20 оттисков.
Здесь представлен один из двух видов "неевклидового" пространства, описанных французским математиком Пуанкаре.
Чтобы понять особенности этого пространства, представьте, что вы находитесь внутри самой картины. По мере вашего перемещения от центра круга к его границе ваш рост будет уменьшаться также, как уменьшаются рыбы на данной картине. Таким образом, путь, который вам надо будет пройти до границы круга будет казаться вам бесконечным.
На самом деле, находясь в таком пространстве, вы на первый взгляд не заметите ничего необычного в нем по сравнению с обычным евклидовым пространством. Например, чтобы достичь границ евклидового пространства вам также необходимо пройти бесконечный путь.
Однако, если внимательно присмотреться, то можно будет заметить некоторые отличия, например, все подобные треугольники имеют в этом пространстве одинаковый размер, и вы не сможете там нарисовать фигуры с четырьмя прямыми углами, соединенными прямыми линиями.

Предел – круг IV (рай и ад), 1960 г.
Продольная гравюра (две доски).
Диаметр 41,5 см.
Предел – круг IV (рай и ад)
И здесь размер компонентов уменьшается по мере центробежного движения к краям круга. 6 самых больших форм (3 белых ангела и 3 черных дьявола) лучами расходятся от центра.
Диск разделен на 6 секций, где доминируют ангелы на черном фоне и дьяволы – на белом. Таким образом, рай и ад меняются местами 6 раз. В промежуточных, «земных» стадиях они подобны друг другу.
Фигуры ангелов и дьяволов, вплотную примыкая друг к другу, заполняют плоскость. При движении от центра гравюры к ее краю фигуры уменьшаются, превращаясь в бесконечное множество фигурок, невидимых невооруженным глазом на самом краю. Этот замечательный орнамент основан на вполне математической идее – известной из евклидовой модели неевклидовой гиперболической плоскости, придуманной Анри Пуанкаре.

Водопад, 1961 г.
Литография. 38х30 см.
Музей Израиля
Водопад
Водопад имеет структуру «невозможного» треугольника Пенроуза: литография была создана по мотивам статьи в «Британском журнале психологии».
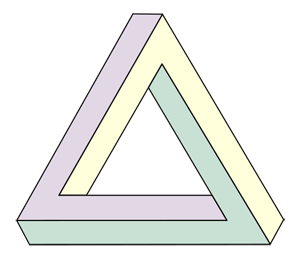
Треугольник (1958 г.)
английского математика
Роджера Пенроуза
Конструкция "Водопада" составлена из перекладин, положенных одна на другую под прямым углом. Следя глазами за всеми ее элементами поочередно, мы не заметили ни малейшего несоответствия между ними.
Однако перд нами – совершенно невозможное целое, поскольку в интерпритации расстояния между обьектом и наблюдателем возникают неожиданные изменения. Эта немыслемая конструкция трижды «вмонтирована» в картину.
Падающая вода приводит в движение мельничное колесо и течет по наклонному зигзагообразному желобу между двумя башнями, возвращаясь к точке, где водопад начинается снова. Мельнику достаточно время от времени плеснуть туда ведерко воды, чтобы компенсировать испарение.
Кажется, что обе башни одинаковой высоты; тем не менее, та что справа, оказывается этажом ниже, чем башня слева.

Меньше и меньше, 1956 г.
Гравюра на дереве
Меньше и меньше
Гравюра «Меньше и меньше» показывает типичный фрактальный объект.
Мауриц Эшер одним из первых стал изображать в своих мозаичных картинах фракталы.
Во время XII Всемирного Математического Конгресса в Амстердаме в 1954 году была открыта выставка работ Эшера. Математическое описание фракталов было предложено только в 1970-е годы (термин «фрактал» был введён в 1975 году).

